Check distribution

In my opinion, the first thing to do when you have several numeric variables is to observe their distribution one by one. This can be done using a violin plot, a boxplot or a ridgeline plot if your variables are all on the same scale. In the case of the mtcars dataset the variables are completely different one to each other so it make more sense to make an histogram for each of them:

# Keep the numeric variables of the mtcars dataset
data <- mtcars %>% select( disp, drat, hp, mpg, qsec, wt)

# Show the histogram of these variables
data %>%
  as.tibble() %>%
  gather(variable, value) %>%
  ggplot( aes(x=value) ) +
    geom_histogram( fill= "#69b3a2") +
    facet_wrap(~variable, scale="free") +
    theme_ipsum()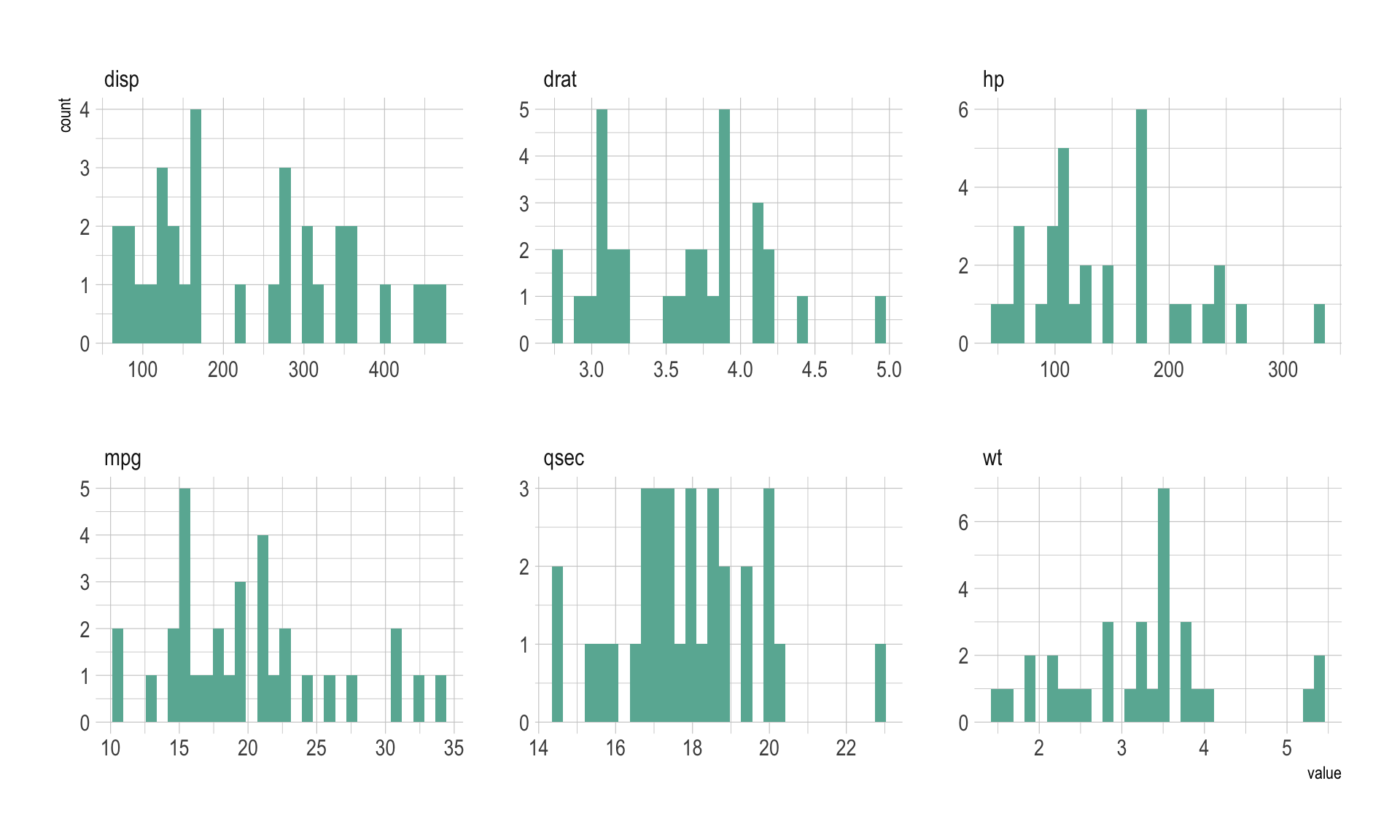

Correlogram

A correlogram or correlation matrix allows to analyse the relationship between each pair of numeric variables of a dataset. The relationship between each pair of variable is visualised through a scatterplot, or a symbol that represents the correlation (bubble, line, number..). The diagonal often represents the distribution of each variable, using an histogram or a density plot.

scatterplotMatrix(~mpg+disp+drat+hp+qsec+wt, data=data , reg.line=FALSE, col="#69b3a2", id.col="#69b3a2", smooth=FALSE , cex=1.5 , pch=20 )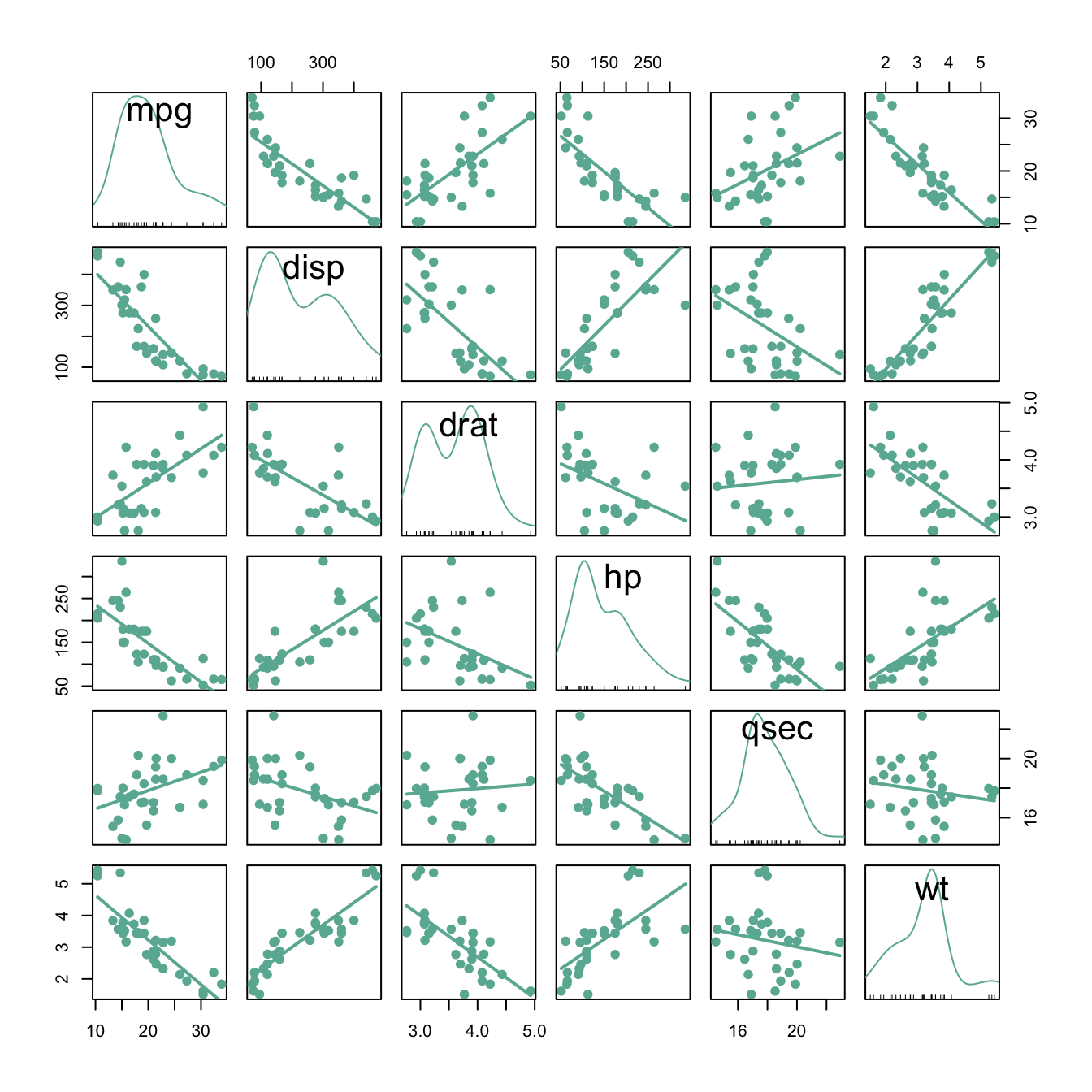

It is a powerful method that give a good overview of the dataset in an unique graphic. For instance, it is obvious that displacement (disp) and gross horsepower (hp) have a strong correlation.

Dendrogram

A dendrogram can be used to check the result of a clustering algorythm on the dataset. Basically, the steps are:

• compute the distance between each pair of sample using correlation or euclidean distance.
• perform clustering on this matrix: it builds a hierarchy of clusters: groups sample that are close one from another
• show the result as a dendrogram:

# Clusterisation using 3 variables
data %>% dist() %>% hclust() %>% as.dendrogram() -> dend

# Color in function of the cluster
par(mar=c(1,1,1,7))
dend %>%
  set("labels_col", value = c("#69b3a2", "#404080", "orange"), k=3) %>%
  set("branches_k_color", value = c("#69b3a2", "#404080", "orange"), k = 3) %>%
  plot(horiz=TRUE, axes=FALSE)
abline(v = 350, lty = 2)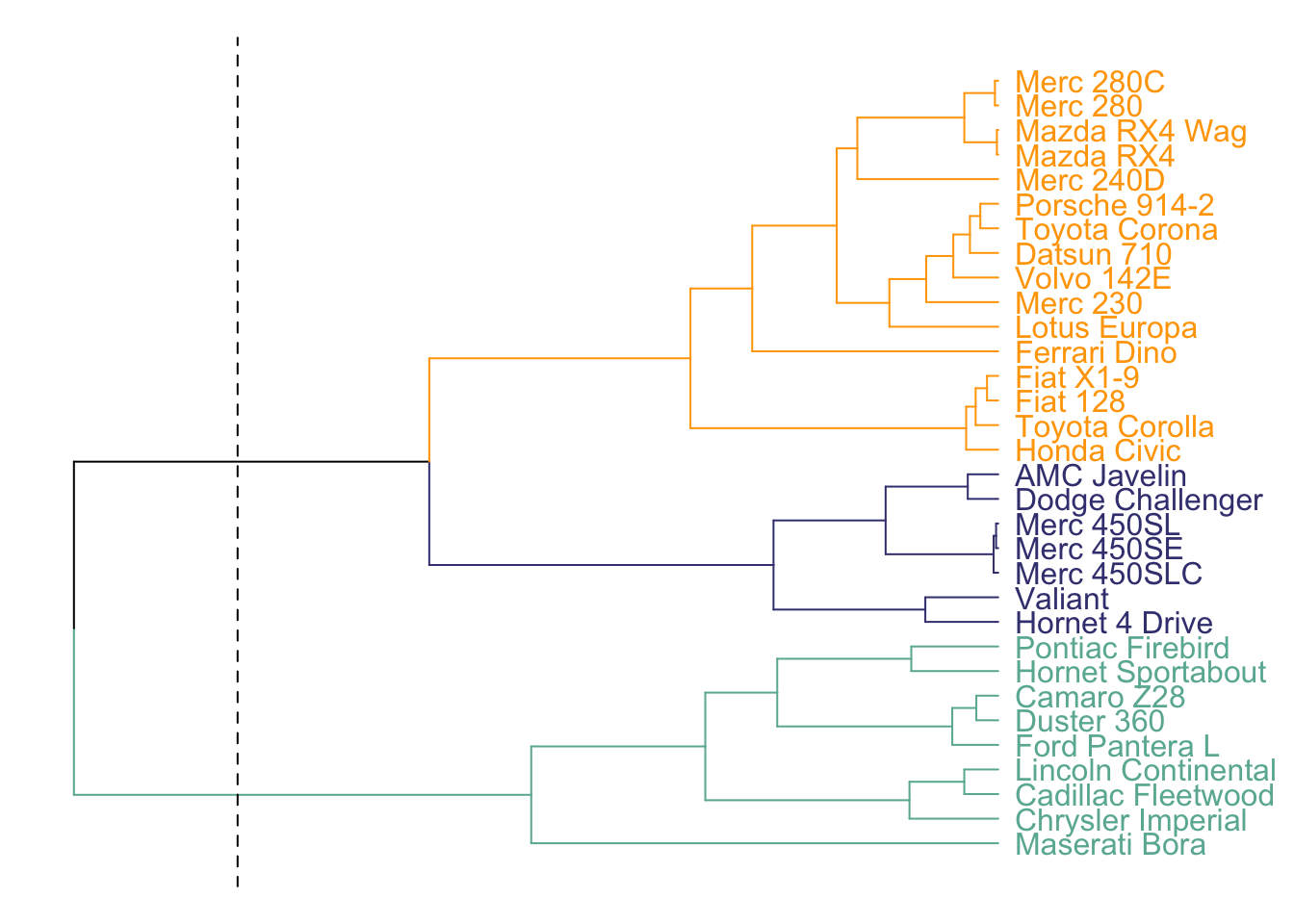

Here, the dendrogram informs us that the Mercedes 280 and the Mercedes 280C have similar features, what makes sense. Basically, it gives an idea of group of cars that are similar one another.

See more about it here.

Heatmap

The heatmap is often used in complement of a dendrogram. It is a graphical representation of data where the individual values contained in a matrix are represented as colors. It is a bit like looking a data table from above.

In addition of a dendrogram, it allows to understand why samples ore features are grouped together.

library(d3heatmap)
d3heatmap(data, k_row = 4, k_col = 2, scale = "column")

The heatmap above allows to understand why cars are split in 2 main clusters. For instance the weight (wt) is much higher for the group on top than for the other.

PCA

The Principal Component Analysis is a statistical procedure that aims to summarize all the available numeric variables in a set of principal components.

myPCA <- PCA(data, scale.unit=TRUE, graph=F)

myPCA$ind %>%
  as.data.frame() %>%
  mutate(name=rownames(.)) %>%
  ggplot( aes(x=coord.Dim.1, y=coord.Dim.2, label=name)) +
    geom_point( color="#69b3a2") +
    theme_ipsum() +
    geom_label(color="#69b3a2")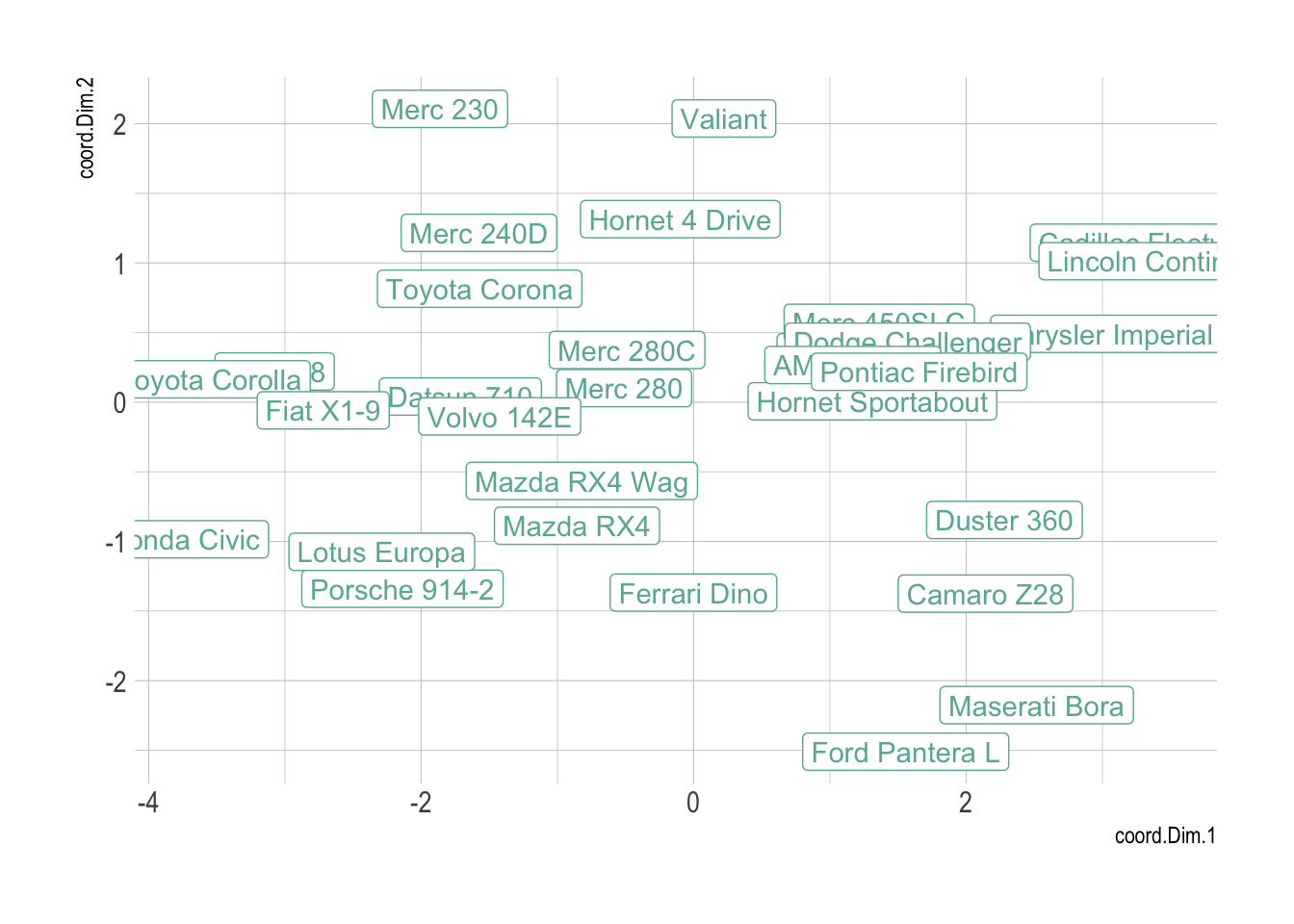

#plot.PCA(myPCA, axes=c(1, 2), choix="var")

Note: this section needs improvement

Getting a correlation matrix

It is of importance to note that this kind of dataset can be converted to a correlation matrix that is an adjacency matrix. Indeed, we can compute the correlation between each pair of variable or each pair of entities of the dataset and try to visualize this new dataset. But this is a new story: how to visualize an adjacency matrix.